|
引用 | 編輯
ebolaman
2011-07-20 15:57 |
1樓
▲ |
|
這只是我的構想而已 (請參考):
將程序分成幾部份,每部分做自己的事,極度模組化: (1) 建構模組 (讀取模組的邊緣線,將部分合成集團,然後用一些曲線去修正邊緣) (2) 模組繪圖 (3) 移動模組 (4) 判斷碰撞 因為現在只討論 "判斷碰撞",所以第五項不考慮 模組 (Model) ,就是構成物體的一整個東西 而模組的邊緣,可以用 函數式來表示 (例如半橢圓 f(x)=Sqrt(1-(x/3)^2) ) 另外一個部分負責 移動模組,那肯定沒問題,而判斷 "何時會碰撞" 會比較困難 正確地來說,應該是要在程式運行中判斷 "已經碰撞了嗎?" 因此,要算數學了 不管是什麼函數,判斷何時有交集最簡單的方法就是 "解聯立" 所以只要一條一條線去互相檢查 "當聯立的解不是無解的時候",就是碰撞發生了 可以下載兩個程式,有助於了解 Physion 與 SpeQ Mathematics SpeQ 是一款數學+圖表的軟體 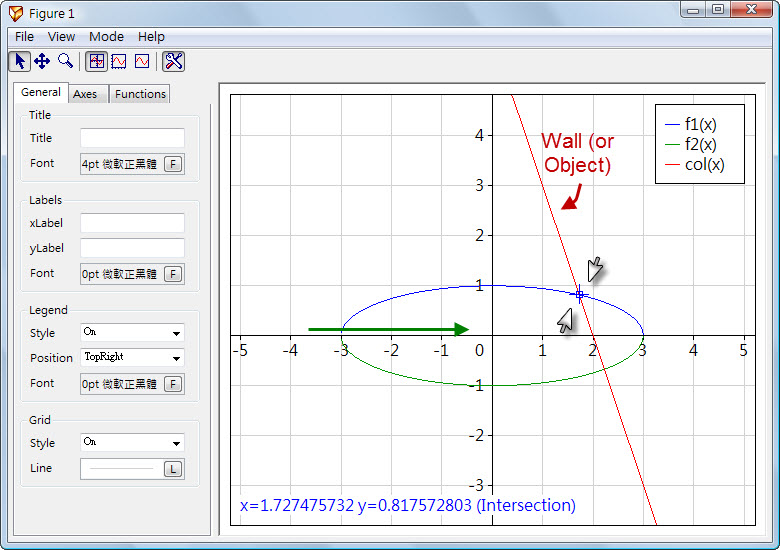 以上的表達式: 複製程式 f1(x)=Sqrt(1-(x/3)^2) f2(x)=-Sqrt(1-(x/3)^2) col(x)=-x*3+6 Plot(f1(x)) Plot(f2(x)) Plot(col(x)) Physion 是一款模擬物理性質的軟體,可以看看這個來構想 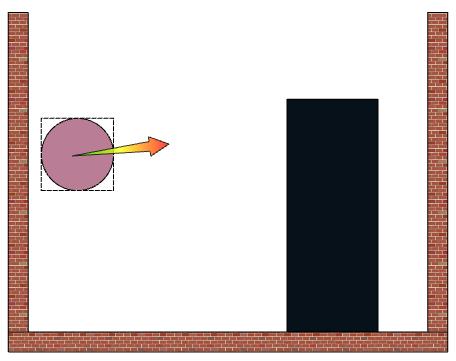  所以實作部分,推薦用線段組成一個正方形,設定四條線是聯合的 加上一個陣列設定每條線初始的運動方向 然後一個 Timer 中規中矩的按照 陣列每個項目的內容去讓 線段移動 (由於四條線組成正方形,因此移動起來還是正方形) Timer 最後還要加上 判斷碰撞 的函數 而這個函數,即是檢查 四條線與另外一條線 (當作牆壁,被撞的物體的一條線) 的聯立方程式是否有解 有解的話還要特別注意 如果物體還會加速,不規則碰撞,運動等 (如果是 傳統貪吃蛇 等速、矩形介面 就不用考慮這點) 因為 Timer 的檢查時間不能太短,在龐大的 2D 繪圖軟體中,如果這樣檢查會浪費效能 (P.S. 可以檢查 X, Y 的值,是先檢查是否有可能交集,有可能再來進入 函數重點部分,例如 一條線 X= 1~3 另外的一條線 X=5~8 這樣就不可能會碰撞) 當有解的時候,通常物體都已經與被碰撞的物體交集有一段時間,所以可以在函數加上 +t 這樣,在已知的會碰撞的時間範圍內,來去解聯立 就能得出正確的碰撞時間與位置 就這樣判斷完成,然後把物體隱藏,或放出 爆炸、粉碎一些 Sprites 特效 其他的就交給繪圖的模組吧 |
|